Standardization and Normalisation
In data processing, feature scaling is an essential step to ensure that different variables within a dataset are on a comparable scale. Since variables often have different ranges, using their original scales can disproportionately impact models, giving more weight to features with larger numerical values. To address this, feature rescaling is applied to independent variables during data preprocessing.
Although the terms normalization and standardization are sometimes used interchangeably, they have distinct meanings. The primary objective of feature scaling is to bring all features to a similar scale, ensuring that they contribute equally and improving the performance of many machine-learning algorithms.
Table of Contents
- What is Standardization?
- What is Normalization?
- Differences Between Standardization and Normalization
- Applications of Standardization and Normalization
- Importance of Standardization and Normalization
- Implementing Standardization and Normalization in Python
- Conclusion
What is Standardization?
Standardization, also known as Z-score normalization, transforms features so that they have a mean of 0 and a standard deviation of 1. This ensures that the data follows a Gaussian distribution with μ = 0 and σ = 1.
This rescaling method is particularly useful for optimization techniques such as gradient descent, which are widely used in machine-learning models that rely on weighted inputs (e.g., linear regression, logistic regression, and neural networks). Additionally, standardization is beneficial for algorithms that use distance-based calculations, such as K-Nearest Neighbors (KNN) and Support Vector Machines (SVMs).
The formula for standardization (Z-score transformation) is:

where:
- XXX is the original feature value,
- μ\muμ is the mean of the feature, and
- σ\sigmaσ is the standard deviation.
This transformation helps ensure that all features are on the same scale, making machine-learning models more effective and reducing biases caused by varying feature ranges.
What is Normalization?
Normalization, also known as Min-Max scaling, is a technique that adjusts feature values so they fall within a fixed range, typically 0 to 1 (or -1 to 1 if negative values are present). This method is particularly useful when standardization is not suitable, such as when the data does not follow a normal distribution or has a very small standard deviation.
By applying normalization, all features are rescaled proportionally, ensuring that no variable dominates due to its original range. This approach is beneficial for algorithms that require bounded input values, such as neural networks and certain clustering techniques.
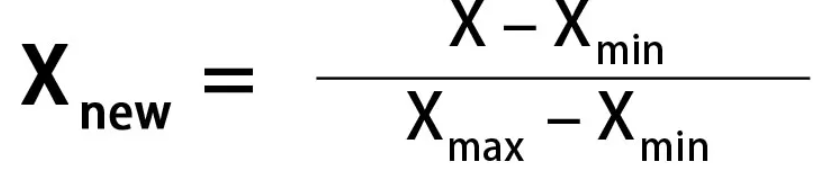
Differences Between Standardization and Normalization
| No. | Normalization | Standardization |
|---|---|---|
| 1 | Uses the minimum and maximum values of features for scaling. | Uses the mean and standard deviation for scaling. |
| 2 | Applied when features have different scales. | Applied to ensure a mean of zero and a standard deviation of one. |
| 3 | Scales values within a fixed range, typically [0,1] or [-1,1]. | Not limited to a specific range. |
| 4 | Highly sensitive to outliers, which can distort scaling. | Less influenced by outliers due to the use of standard deviation. |
| 5 | In Scikit-Learn, the MinMaxScaler is used for normalization. | Scikit-Learn provides the StandardScaler for standardization. |
| 6 | Compresses the data within an n-dimensional unit hypercube. | Shifts the data so that its mean aligns with the origin and then adjusts the scale. |
| 7 | Useful when the distribution of features is unknown. | Works best when the data follows a Normal (Gaussian) distribution. |
| 8 | Also referred to as Scaling Normalization. | Often called Z-Score Normalization. |
This table provides a clear distinction between Normalization and Standardization, helping in choosing the right technique based on the dataset and its properties.
Applications of Standardization and Normalization
Standardization and normalization play a crucial role in machine learning and data preprocessing by improving algorithm efficiency and ensuring that features contribute equally to model training. Here are some key applications:
Gradient Descent Optimization:
- These techniques assist optimization algorithms, such as gradient descent, in converging more efficiently by ensuring a uniform feature scale. This is particularly useful in linear regression, logistic regression, and neural networks.
K-Nearest Neighbors (KNN):
- Since KNN relies on distance calculations, standardization prevents features with larger numerical ranges from disproportionately affecting distance measurements, ensuring accurate classification.
Support Vector Machines (SVM):
- Standardization ensures that features with different scales do not skew the decision boundary, leading to a more balanced and accurate classification.
Principal Component Analysis (PCA):
- PCA is sensitive to the magnitude of features. Standardization ensures that features with larger scales do not dominate the principal components, preserving the true structure of the data.
Neural Networks:
- Normalization, including batch normalization, is commonly applied in deep learning models to stabilize training, speed up convergence, and improve overall performance.
These applications highlight how standardization and normalization enhance machine learning models by improving training efficiency, optimizing performance, and ensuring balanced feature contributions. The choice between the two techniques depends on the specific algorithm and dataset characteristics.
Significance of Standardization and Normalization
The importance of standardization and normalization lies in their ability to enhance model performance, accelerate convergence, and maintain feature balance. Below are some key reasons why these techniques are essential:
Faster Convergence:
- Algorithms that rely on gradient-based optimization, such as gradient descent, perform more efficiently when features have a consistent scale, leading to quicker and more stable convergence.
Reducing Sensitivity to Scale:
- Models like KNN, SVM, and neural networks can be highly sensitive to variations in feature scale. Standardization and normalization mitigate this issue, ensuring no single feature dominates the learning process.
Enhancing Model Accuracy:
- By preventing scale-based biases, these preprocessing techniques improve the predictive performance and reliability of machine learning models.
Ensuring Equal Feature Contributions:
- Standardization and normalization prevent disproportionately large features from influencing the model's decisions, ensuring fair treatment of all input variables.
Improving Interpretability of Model Coefficients:
- In models like linear regression, standardization makes coefficient values comparable, improving interpretability and aiding decision-making.
Implementation standardization and normalization in Python
from sklearn.preprocessing import StandardScaler, MinMaxScaler
import numpy as np
# Sample data (3 samples, 3 features)
data = np.array([[1.0, 2.0, 3.0],
[4.0, 5.0, 6.0],
[7.0, 8.0, 9.0]])
# Initialize the StandardScaler
scaler_standard = StandardScaler()
# Apply standardization: mean=0, variance=1
standardized_data = scaler_standard.fit_transform(data)
# Initialize the MinMaxScaler
scaler_minmax = MinMaxScaler()
# Apply normalization: scales data to range [0, 1]
normalized_data = scaler_minmax.fit_transform(data)
# Display the results
print("Original Data:\n", data)
print("\nStandardized Data (mean=0, std=1):\n", standardized_data)
print("\nNormalized Data (scaled to [0, 1]):\n", normalized_data)
# Additional information to verify the transformations
print("\nMean of Standardized Data (should be close to 0):", np.mean(standardized_data, axis=0))
print("Standard Deviation of Standardized Data (should be 1):", np.std(standardized_data, axis=0))
Conclusion
Standardization and normalization are essential preprocessing techniques in machine learning, significantly contributing to algorithm efficiency, stability, and interpretability. Below are the key reasons why these techniques are important:
Improved Convergence:
- Both methods enhance the training process by ensuring that optimization algorithms, such as gradient descent, converge more quickly and efficiently.
Reducing Sensitivity to Scale:
- These techniques help mitigate the impact of varying feature scales, preventing any single feature from disproportionately influencing model learning.
Enhanced Model Performance:
- By addressing discrepancies in feature magnitudes, standardization and normalization contribute to more stable predictions and improved overall model accuracy.
Equal Feature Contributions:
- Ensuring that all features are treated fairly prevents larger-scaled variables from dominating model outcomes, promoting balanced learning.
Better Interpretability:
- Standardization helps in making model coefficients more interpretable, particularly in linear models, while normalization ensures consistency in feature importance across different models.
As fundamental steps in data preprocessing, these techniques allow machine learning models to handle datasets with diverse characteristics effectively. The choice between standardization and normalization depends on the nature of the dataset and the specific algorithm being used. When applied correctly, these methods improve model reliability, efficiency, and predictive performance across various applications.
Featured Blogs

BCG Digital Acceleration Index

Bain’s Elements of Value Framework

McKinsey Growth Pyramid

McKinsey Digital Flywheel

McKinsey 9-Box Talent Matrix

McKinsey 7S Framework

The Psychology of Persuasion in Marketing

The Influence of Colors on Branding and Marketing Psychology

What is Marketing?
Recent Blogs

Part 8: From Blocks to Brilliance – How Transformers Became Large Language Models (LLMs) of the series - From Sequences to Sentience: Building Blocks of the Transformer Revolution

Part 7: The Power of Now – Parallel Processing in Transformers of the series - From Sequences to Sentience: Building Blocks of the Transformer Revolution

Part 6: The Eyes of the Model – Self-Attention of the series - From Sequences to Sentience: Building Blocks of the Transformer Revolution

Part 5: The Generator – Transformer Decoders of the series - From Sequences to Sentience: Building Blocks of the Transformer Revolution

Part 4: The Comprehender – Transformer Encoders of the series - From Sequences to Sentience: Building Blocks of the Transformer Revolution of the series - From Sequences to Sentience: Building Blocks of the Transformer Revolution


