Principle of Insufficient Reason
The Principle of Indifference, also referred to as the Principle of Insufficient Reason, is a key concept in probability theory and decision-making. It states that in scenarios where there is no valid basis to favor one outcome over another, each possible outcome should be assigned an equal probability. This principle has been widely discussed by mathematicians such as Jacob Bernoulli and Pierre-Simon Laplace and has historically been used in probability assessments, particularly in games of chance.
Origins and Logical Basis
The origins of this principle date back to early probability theory and were formally articulated by Pierre-Simon Laplace in the 18th century. Laplace proposed that in the absence of any information distinguishing one event from another, it is rational to treat all outcomes as equally probable. The reasoning behind this approach is based on logical neutrality—if no evidence suggests a particular outcome is more likely, then assuming equal likelihood is the most impartial stance.
Application in Probability
This principle is often employed in probability theory when prior data is unavailable. For example, when flipping an unbiased coin, there is no reason to expect heads more frequently than tails, so each is assigned a probability of 50%. Similarly, when rolling a fair six-sided die, each face is considered equally probable, with a probability of 1/6.
The principle is particularly useful in setting initial probabilities before empirical data becomes available. This makes it a foundational tool in Bayesian statistics, where prior probabilities are later updated based on observed evidence.
Challenges and Limitations
Despite its theoretical appeal, the Principle of Indifference has sparked debate due to its potential inconsistencies. One of its main criticisms arises from the way probabilities can shift depending on how the problem is framed. For instance, estimating the probability of rain tomorrow by considering only two possible states—rain or no rain—yields a probability of 50%. However, introducing a third possibility, such as snow, alters the probability distribution, reducing the likelihood of each individual outcome.
Another challenge is its application in continuous probability distributions, where defining equally probable outcomes is not straightforward. Additionally, different ways of partitioning a problem can lead to contradictory probability assignments. The principle’s reliance on subjective interpretation—determining which outcomes are “equally likely”—can further complicate its application.
Practical Use and Relevance
Despite its drawbacks, the Principle of Indifference remains relevant in fields such as decision theory and Bayesian analysis. In decision-making under uncertainty, it provides a rational method for assigning initial probabilities before empirical data is available. In Bayesian statistics, it guides the selection of non-informative priors, ensuring an unbiased starting point for probability estimation.
In practice, the principle serves as a useful but provisional tool. While it offers a logical foundation for initial probability assignments, it should be applied with caution and refined as new information becomes available. Awareness of its potential pitfalls helps avoid misinterpretations and ensures more accurate probability assessments over time.
Conclusion
The Principle of Indifference plays a fundamental role in probability theory by providing a rational approach to uncertainty when no prior information is available. However, its limitations highlight the need for careful application and continuous reassessment as new data emerges. While it is a valuable starting point, its use must be tempered with an understanding of its potential inconsistencies and subjectivity. By applying this principle judiciously, one can make more informed and reliable probability-based decisions.
Featured Blogs
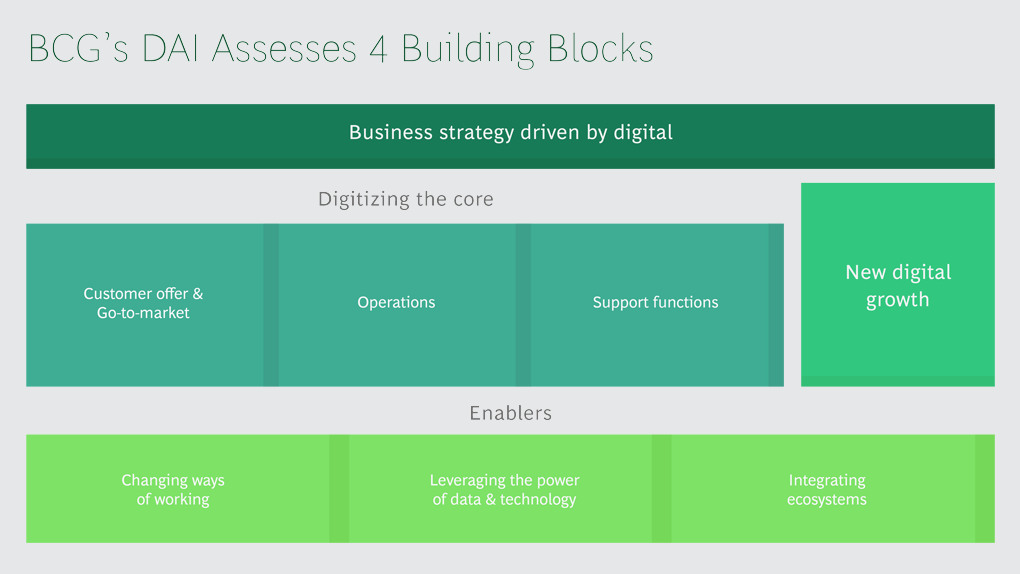
BCG Digital Acceleration Index
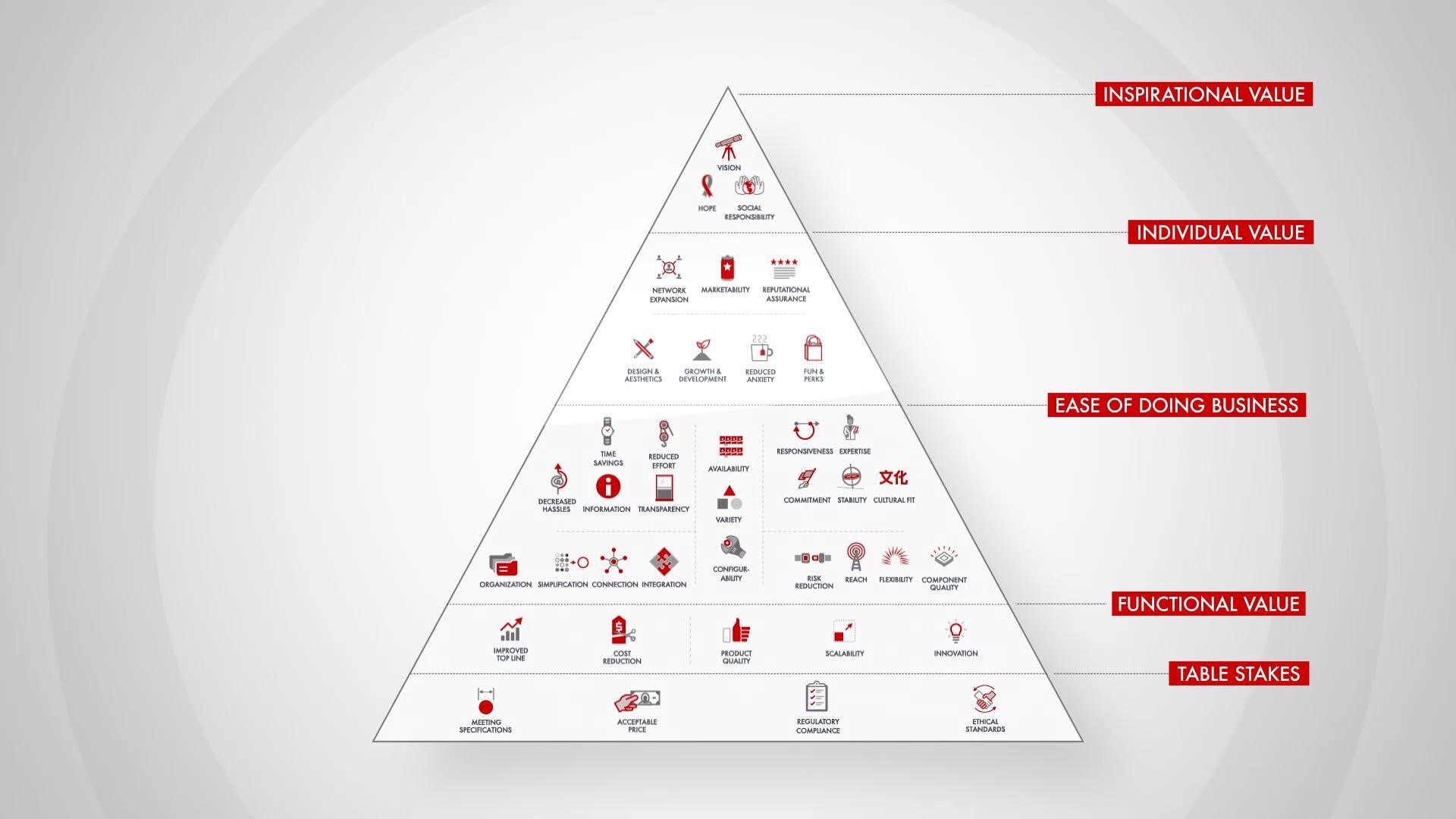
Bain’s Elements of Value Framework
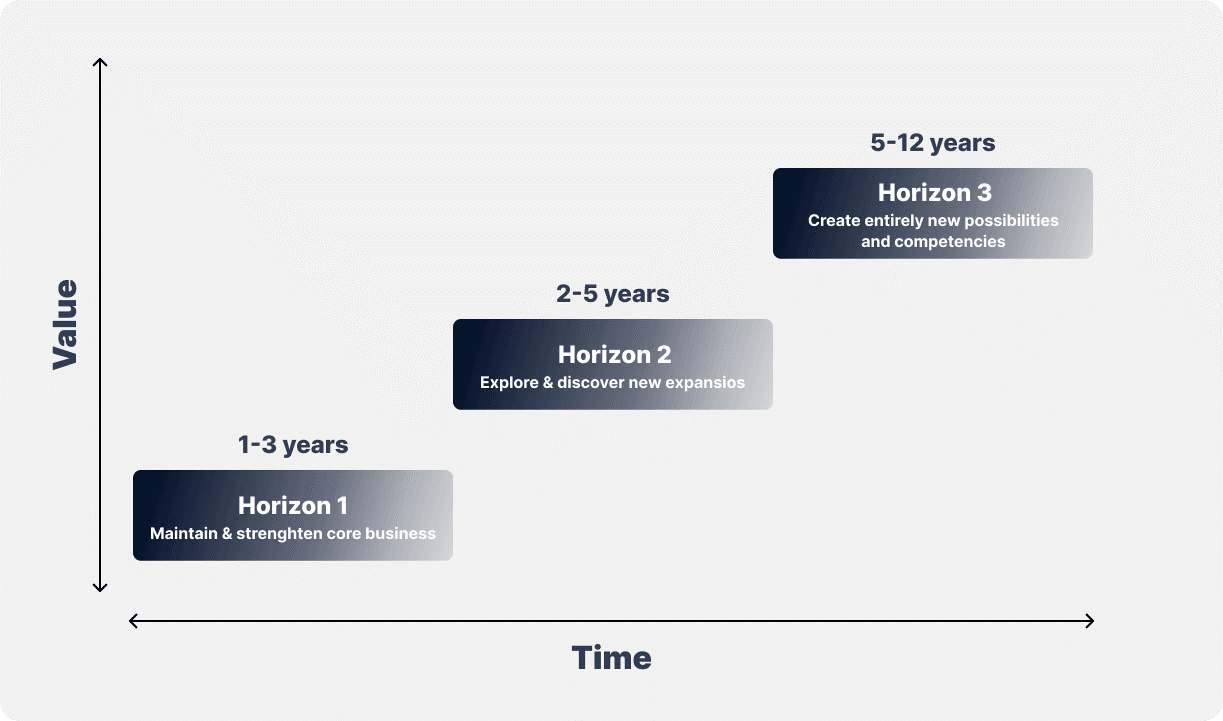
McKinsey Growth Pyramid
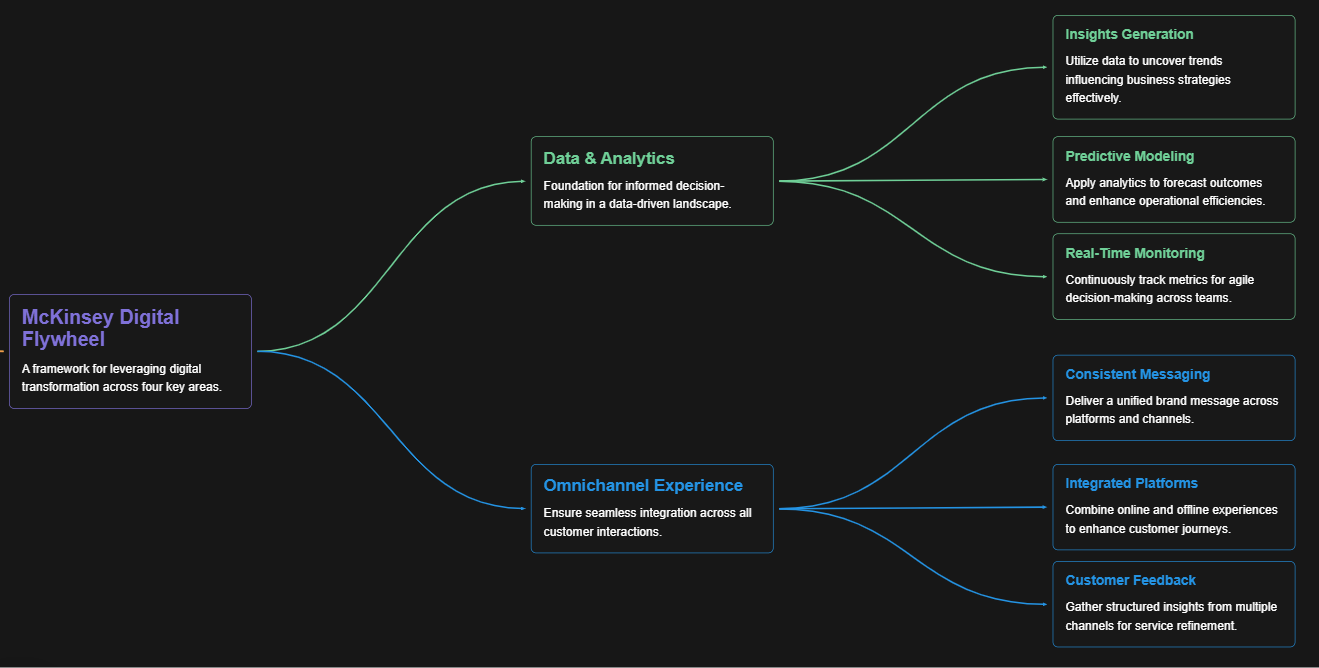
McKinsey Digital Flywheel

McKinsey 9-Box Talent Matrix
McKinsey 7S Framework
The Psychology of Persuasion in Marketing

The Influence of Colors on Branding and Marketing Psychology

What is Marketing?
Recent Blogs

Part 8: From Blocks to Brilliance – How Transformers Became Large Language Models (LLMs) of the series - From Sequences to Sentience: Building Blocks of the Transformer Revolution

Part 7: The Power of Now – Parallel Processing in Transformers of the series - From Sequences to Sentience: Building Blocks of the Transformer Revolution
Part 6: The Eyes of the Model – Self-Attention of the series - From Sequences to Sentience: Building Blocks of the Transformer Revolution

Part 5: The Generator – Transformer Decoders of the series - From Sequences to Sentience: Building Blocks of the Transformer Revolution

Part 4: The Comprehender – Transformer Encoders of the series - From Sequences to Sentience: Building Blocks of the Transformer Revolution of the series - From Sequences to Sentience: Building Blocks of the Transformer Revolution


