Applications of Copula
In a world overflowing with data, understanding the relationships between variables is paramount. While correlation has long been the go-to metric, it often fails to capture the intricate dependencies that exist in real-world phenomena. This is where copulas emerge as invaluable tools, providing a flexible and elegant framework for modelling complex relationships across diverse domains.
This article delves deep into the world of copulas, exploring their mathematical underpinnings, diverse applications, and the exciting possibilities they unlock for analysis and decision-making.
Table of Contents
- Deconstructing Dependency: The Essence of Copulas
- Applications in Finance and Risk Management
- Applications in Insurance and Actuarial Science
- Applications in Engineering and Environmental Science
- Applications in Machine Learning and Data Science
- Applications in Healthcare and Biostatistics
- Challenges and Future Directions
- Conclusion
Deconstructing Dependency: The Essence of Copulas
Imagine two islands, each representing the unique behaviour of a variable, like stock prices or rainfall patterns. Correlation would be like a simple bridge connecting these islands, only reflecting linear associations. However, real-world dependencies are rarely that straightforward.
Copulas act as sophisticated bridges, not only connecting the islands (marginal distributions) but also capturing the intricate shape of their interconnectedness. They achieve this by separating the individual behaviour of each variable from their joint dependency structure.
Applications in Finance and Risk Management
Portfolio Optimization:
Copulas provide a more realistic representation of asset return dependencies, particularly during market downturns when correlations tend to break down. This allows investors to construct more robust portfolios by considering tail dependencies and optimizing asset allocation for different risk appetites.Credit Risk Modelling:
Traditional credit risk models often assume independence between borrowers, which can lead to underestimation of potential losses. Copulas enable the modelling of joint default probabilities, providing a more accurate assessment of portfolio credit risk and facilitating better risk mitigation strategies.Value-at-Risk (VaR) Estimation:
VaR, a crucial metric for financial risk management, estimates the potential loss of a portfolio over a specific timeframe. Copulas enhance VaR calculations by capturing tail dependencies, providing a more comprehensive picture of risk exposure, especially during extreme market events.Stress Testing:
Copulas enable the simulation of various market scenarios with different dependency structures, allowing financial institutions to assess the resilience of their portfolios under adverse conditions and develop effective contingency plans.
Applications in Actuarial Science
Pricing and Reserving:
Copulas enable the joint modelling of claim sizes and frequencies, crucial for accurately pricing insurance contracts and setting appropriate reserves for future liabilities. This leads to more competitive premiums for policyholders and financial stability for insurance companies.Dependency Modelling in Life Insurance:
Copulas can model the dependence between the lifetimes of multiple individuals, vital for pricing joint-life insurance products and calculating annuities. This ensures fair pricing and sustainable product offerings for customers.Extreme Event Modelling:
In areas like catastrophe insurance, copulas help model the dependence between different perils (e.g., hurricanes and floods) to estimate the likelihood and potential impact of simultaneous events, enabling better risk assessment and pricing.
Applications in Engineering and Environmental Science
Hydrological modelling:
Accurately capturing the joint distribution of rainfall intensity and duration is crucial for flood prediction and water resource management. Copulas excel in modelling such dependencies, leading to improved flood forecasting, optimized dam operations, and enhanced water resource allocation.Reliability Engineering:
Copulas are employed to model the dependence between component failures in complex systems, such as power grids or aircraft engines. This facilitates more accurate reliability assessments, optimal maintenance schedules, and informed decision-making regarding system design and redundancy.Environmental Risk Assessment:
Understanding the joint occurrence of extreme environmental events, like heatwaves and droughts, is crucial for risk mitigation and disaster preparedness. Copulas provide a powerful tool for modelling these dependencies, contributing to better risk assessment, informed policymaking, and effective adaptation strategies.
Applications in Machine Learning and Data Science
Data Generation:
Copulas enable the generation of synthetic datasets with specific dependence structures, mimicking real-world complexities. This proves invaluable in situations where real data is scarce or unavailable, facilitating model development, testing, and validation.Outlier Detection:
By capturing the expected dependence patterns between variables, copulas can identify data points that deviate significantly from the norm. This aids in detecting potential anomalies or outliers in datasets, improving data quality and enhancing model accuracy.Feature Selection and Transformation:
Copula-based methods can identify and select relevant features in high-dimensional datasets by capturing important dependencies. This leads to more efficient and accurate machine learning models, reducing computational costs and improving predictive power.
Applications in Healthcare and Biostatistics
Disease modelling and Prediction:
Copulas can model the complex relationships between various risk factors and disease occurrence, facilitating more accurate disease prediction models. This allows for personalized risk assessment, targeted interventions, and improved patient outcomes.Survival Analysis:
In clinical trials and epidemiological studies, copulas are employed to analyse the time-to-event data, considering potential dependencies between survival times of patients with different characteristics. This provides valuable insights into treatment efficacy and disease progression.Joint modelling of Longitudinal and Survival Data:
Copulas enable the simultaneous analysis of longitudinal data (e.g., biomarker measurements over time) and survival data, capturing the dynamic relationship between them. This facilitates a more holistic understanding of disease progression and treatment effects.
Challenges and Future Directions
While immensely powerful, copulas are not without challenges. Selecting the most appropriate copula model for a given dataset remains a complex task, requiring careful consideration of data characteristics and model assumptions. Additionally, dealing with high-dimensional data can pose computational challenges, necessitating the development of efficient estimation techniques and algorithms.
Despite these challenges, the future of copula modelling is bright. Ongoing research focuses on:
Developing new copula families
to capture an even wider range of dependency structures and address specific application needs.Improving estimation techniques
to enhance accuracy and computational efficiency, particularly for high-dimensional data.Exploring the integration of copulas
with other advanced statistical and machine learning techniques to further enhance their capabilities and expand their applications.
Conclusion
Copulas offer a powerful and versatile framework for moving beyond simple correlation and embracing the complexities of real-world dependencies. Their ability to model intricate relationships between variables has led to significant advancements across diverse fields, from finance and insurance to engineering and healthcare. As researchers continue to refine existing techniques and explore new applications, we can anticipate copulas playing an increasingly vital role in shaping our understanding of complex systems and guiding informed decision-making in an increasingly interconnected world.
Featured Blogs
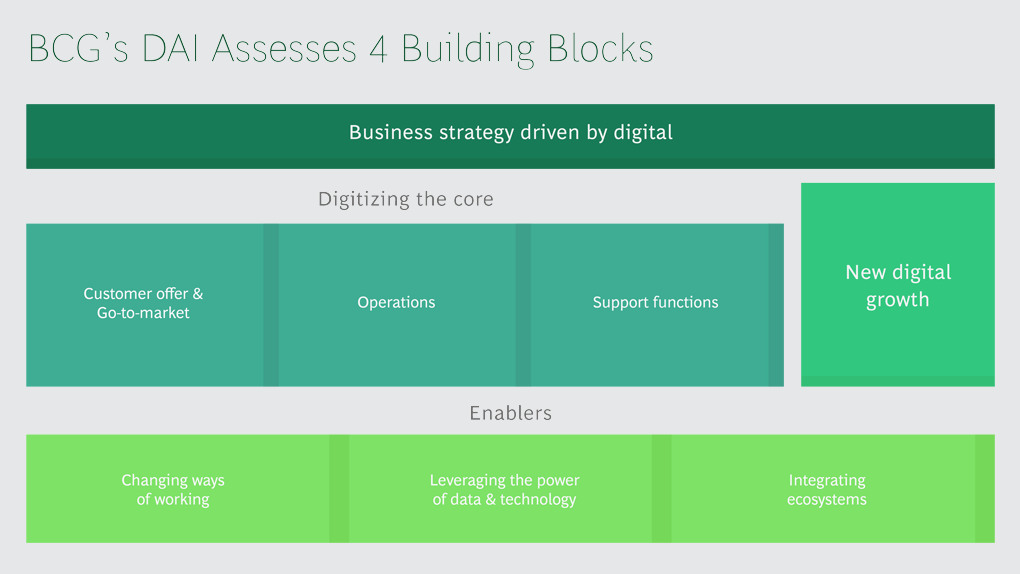
BCG Digital Acceleration Index
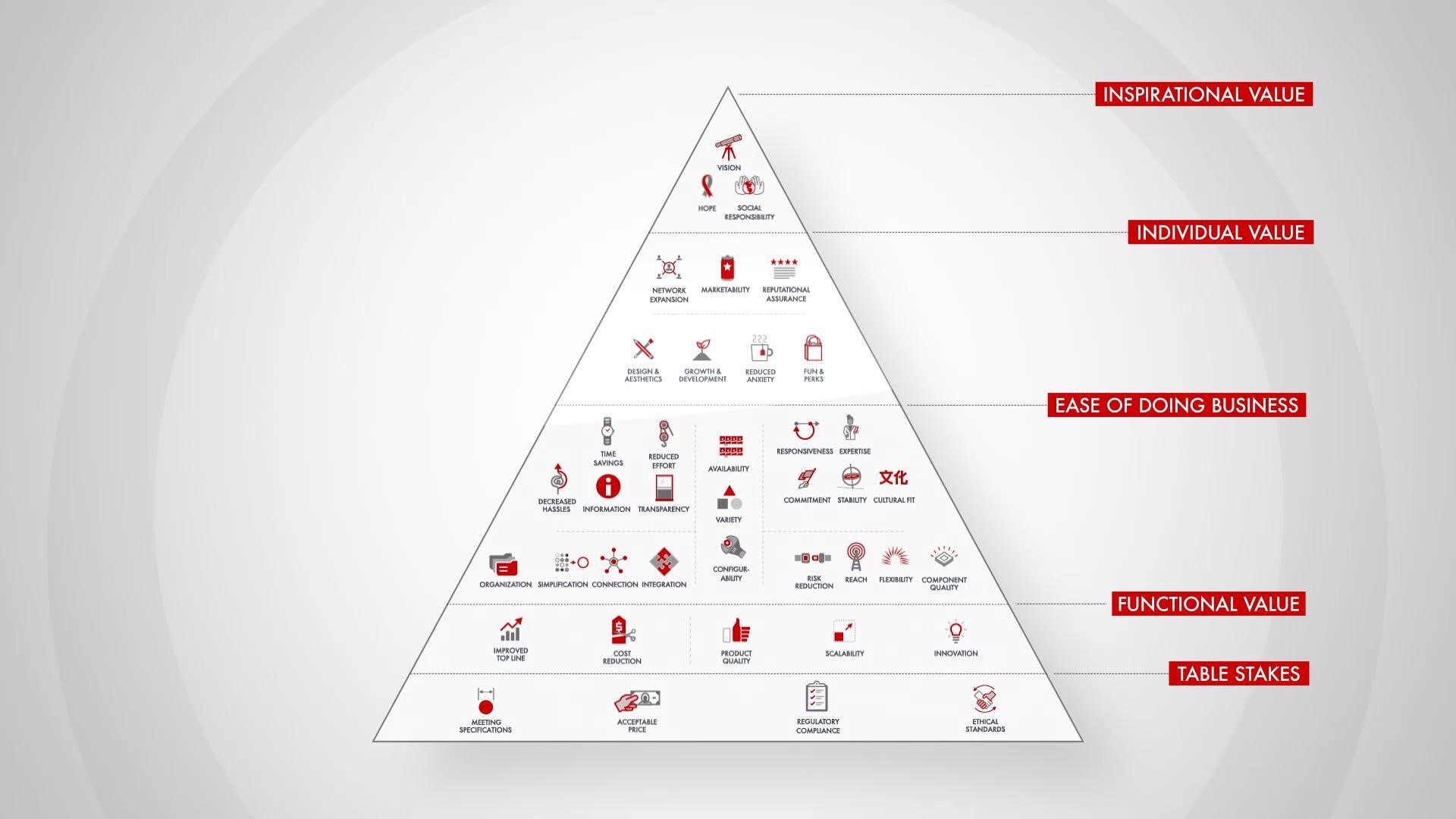
Bain’s Elements of Value Framework
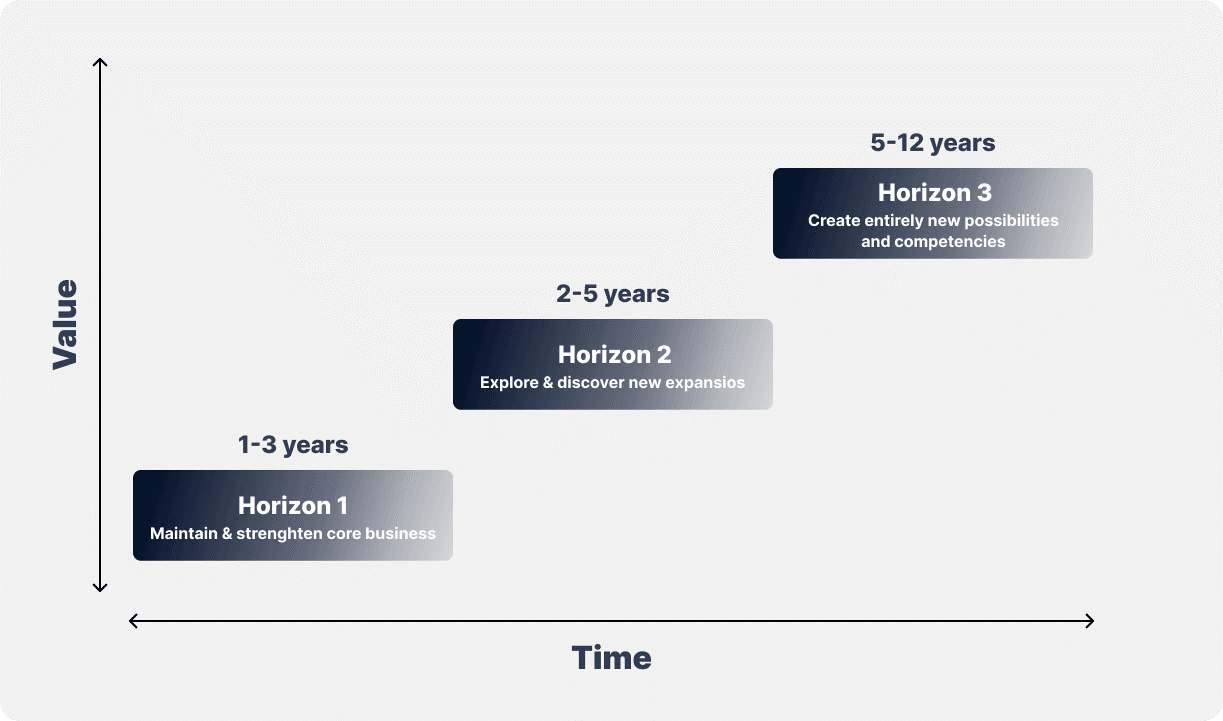
McKinsey Growth Pyramid
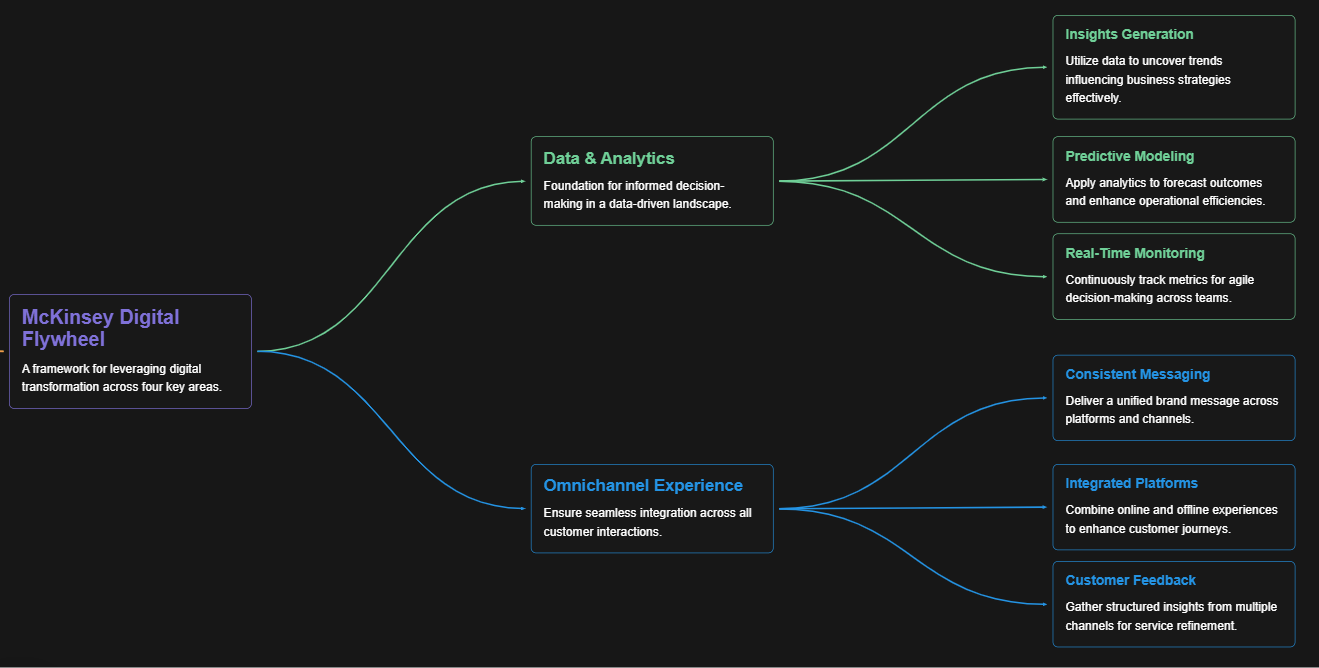
McKinsey Digital Flywheel

McKinsey 9-Box Talent Matrix
McKinsey 7S Framework
The Psychology of Persuasion in Marketing

The Influence of Colors on Branding and Marketing Psychology

What is Marketing?
Recent Blogs

Part 8: From Blocks to Brilliance – How Transformers Became Large Language Models (LLMs) of the series - From Sequences to Sentience: Building Blocks of the Transformer Revolution

Part 7: The Power of Now – Parallel Processing in Transformers of the series - From Sequences to Sentience: Building Blocks of the Transformer Revolution
Part 6: The Eyes of the Model – Self-Attention of the series - From Sequences to Sentience: Building Blocks of the Transformer Revolution

Part 5: The Generator – Transformer Decoders of the series - From Sequences to Sentience: Building Blocks of the Transformer Revolution

Part 4: The Comprehender – Transformer Encoders of the series - From Sequences to Sentience: Building Blocks of the Transformer Revolution of the series - From Sequences to Sentience: Building Blocks of the Transformer Revolution


