Logistic Regression and Odds Ratio

Logistic Regression and Odds Ratio

Logistic regression is a statistical method used to model binary outcome variables, where the response variable is categorical with two possible outcomes, typically coded as 0 and 1. It is widely used for classification problems. The odds ratio is a measure derived from logistic regression, quantifying the association between the independent variables and the binary outcome, offering a clear interpretation of the likelihood of different outcomes.

Table of Contents

1. Introduction to Logistic Regression
2. Logistic Regression Model
3. Understanding Odds Ratio
4. Calculation of Odds Ratio
5. Significance of Logistic Regression and Odds Ratio
6. Applications of Logistic Regression and Odds Ratio
7. Implementation in Python
8. Conclusion

Introduction to Logistic Regression

Logistic regression is a foundational tool in statistical analysis and machine learning, particularly for binary classification tasks. Unlike linear regression, which predicts continuous outcomes, logistic regression predicts the probability that a given input point belongs to a category. This method transforms linear combinations of input features using the logistic function, ensuring the prediction is always between 0 and 1.

Logistic Regression Model

In logistic regression, the dependent variable Y is categorical, and the predictors X1​,X2​,...,Xn​ can be continuous or categorical. The logistic function is defined as:

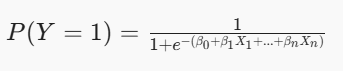
Where P(Y=1) is the probability of the event occurring, and β0​,β1​,...,βn​ are the model coefficients.

Understanding Odds Ratio

The odds ratio (OR) is a statistic that quantifies the strength and direction of the association between predictors and the response variable in logistic regression:

• Odds:

  The odds of an event is defined as the probability of the event occurring divided by the probability of it not occurring.

• Odds Ratio:

  Compares the odds of the event occurring for different levels of an explanatory variable.

An odds ratio greater than 1 indicates a positive association; less than 1 indicates a negative association, and equal to 1 implies no association.

Calculation of Odds Ratio

In logistic regression, the odds ratio for a predictor XiXi​ can be calculated as:

OR=e^βi​

Where βi​ is the coefficient of the predictor from the logistic regression model. This exponentiation transforms the log-odds scale back to the odds ratio scale, allowing for interpretation.

Significance of Logistic Regression and Odds Ratio

• Predictive Insights:

  By modelling binary outcomes, logistic regression provides predictive insights across various applications.

• Intuitive Interpretation:

  The odds ratio provides a straightforward interpretation of how each predictor influences the outcome, aiding in strategic decision-making.

• Hypothesis Testing:

  Logistic regression and odds ratios enable testing hypotheses about relationships between variables.

Applications of Logistic Regression and Odds Ratio

• Healthcare:

  Used to predict disease presence or absence, evaluate risk factors, and interpret relationships in epidemiological studies.

• Finance:

  Assists in credit scoring, risk assessment, and predicting default likelihood.

• Marketing:

  Helps in customer segmentation, targeting strategies, and predicting customer churn.

• Social Sciences:

  Applied in survey analysis, decision-making studies, and behavioural predictions.

Implementation in Python

import pandas as pd
from sklearn.linear_model import LogisticRegression
import numpy as np
# Sample data for illustration
data = {
'Feature1': [2, 3, 5, 7, 9],
'Feature2': [1, 0, 1, 0, 1],
'Outcome': [0, 0, 1, 1, 1]
}
df = pd.DataFrame(data)
# Features and target variable
X = df[['Feature1', 'Feature2']]
y = df['Outcome']
# Logistic Regression Model
model = LogisticRegression()
model.fit(X, y)
# Calculating odds ratios
odds_ratios = np.exp(model.coef_)[0]
features = X.columns
# Print odds ratios for each feature
print("Odds Ratios:")
for feature, odds in zip(features, odds_ratios):
print(f"{feature}: {odds:.2f}")

Conclusion

Logistic regression and odds ratios are powerful statistical tools that facilitate understanding and modelling of binary outcomes. By providing clear insights into variable associations, they play a crucial role in decision-making across various domains. Proper implementation and interpretation of these methods can significantly enhance predictive modelling and strategic insights.